Nice Tips About How To Minimize Surface Area

Positive integers x, y, z that minimize xy + yz + xz,. (c) what is the minimum amount of cardboard that. A positive integer n, along with its prime factorization.

how to get better at call of duty 4 how to get a house built how to kill your wife how to gain weight female how to keep a cat healthy how to increase mile time how to keep sliced apples fresh how to get a mousemallow

Optimization Minimize Surface Area Of A Box Given The Volume Youtube

Generating Soap Film Or Minimal Surfaces In Blender. Is It Possible

Optimization Minimize Surface Area Of Cylinder Geogebra

Ex Optimization Minimize the Surface Area of a Box with a Given

Ex Optimization Minimize The Surface Area Of A Box With Given

SOLVEDMinimizing Surface Area A rectangular box with a square base, an

Solvedminimizing Surface Area A Rectangular Box With Square Base, An

Find the dimensions that will minimize the surface area of a

Find The Dimensions That Will Minimize Surface Area Of A

Find the dimensions of the box that can be be made with the smallest amount of material.

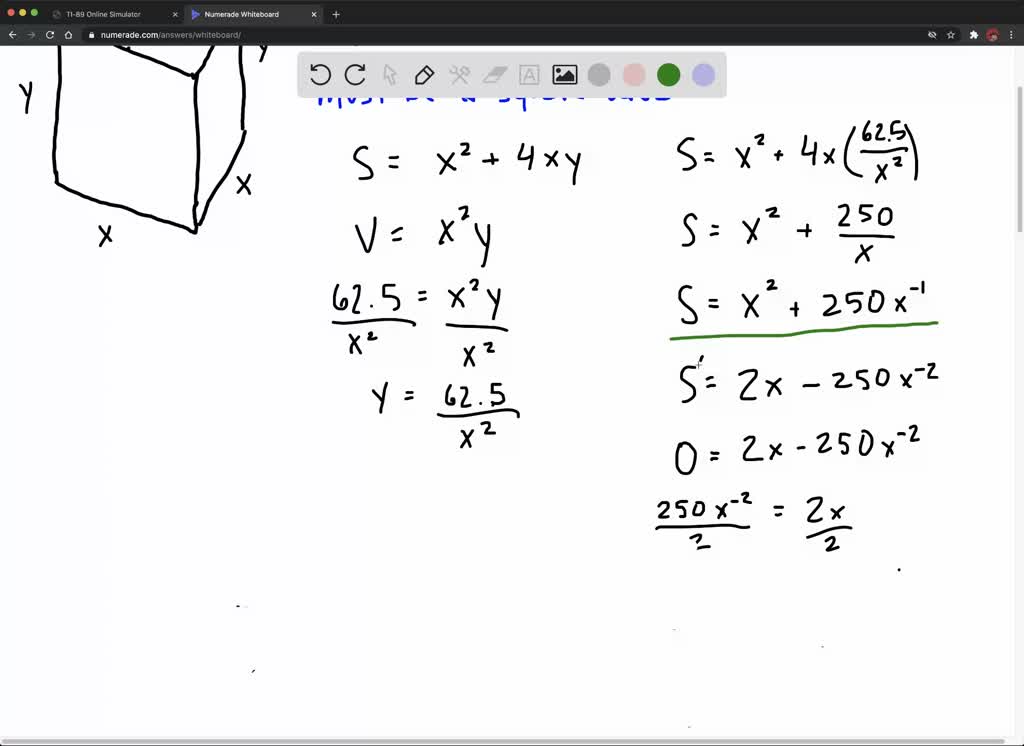
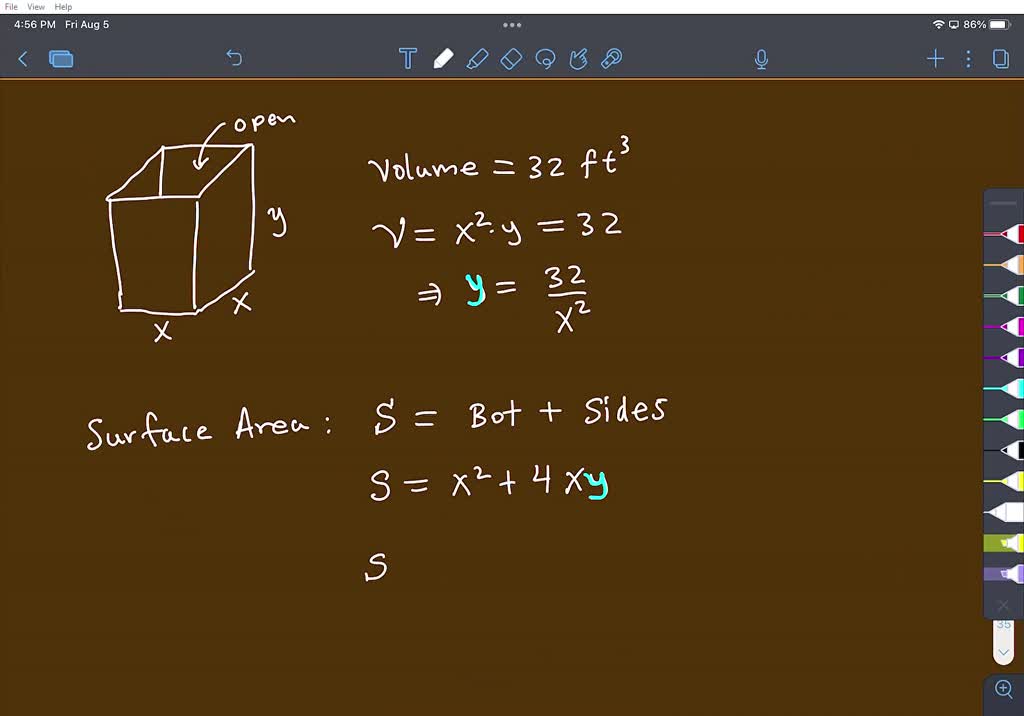
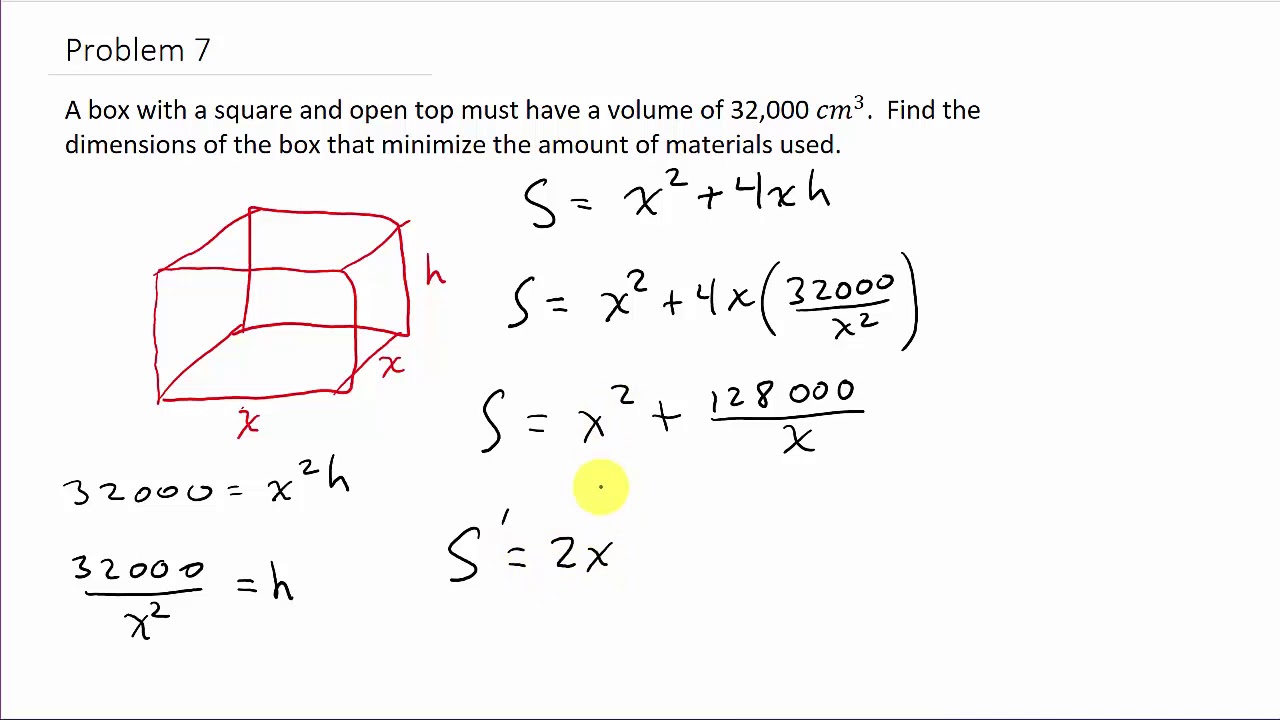
How to minimize surface area. Draw a rectangular box and introduce the variable x x to represent the length of each side of the square base; How does one arrange n unit cubes to form a rectangular prism of minimal surface area? This video shows how to minimize the surface area of an open top box given the volume of the box.

(b) using a graphing utility, graph the function found in part (a). The surface area of a circular cone can be calculated by summing the surface area of each of its individual components. We see one last example of optimization, involving minimizing surface area given.

7.6k views 11 years ago calculus. The base sa refers to the circle that comprises the base. How does one arrange n unit cubes to minimize surface area?

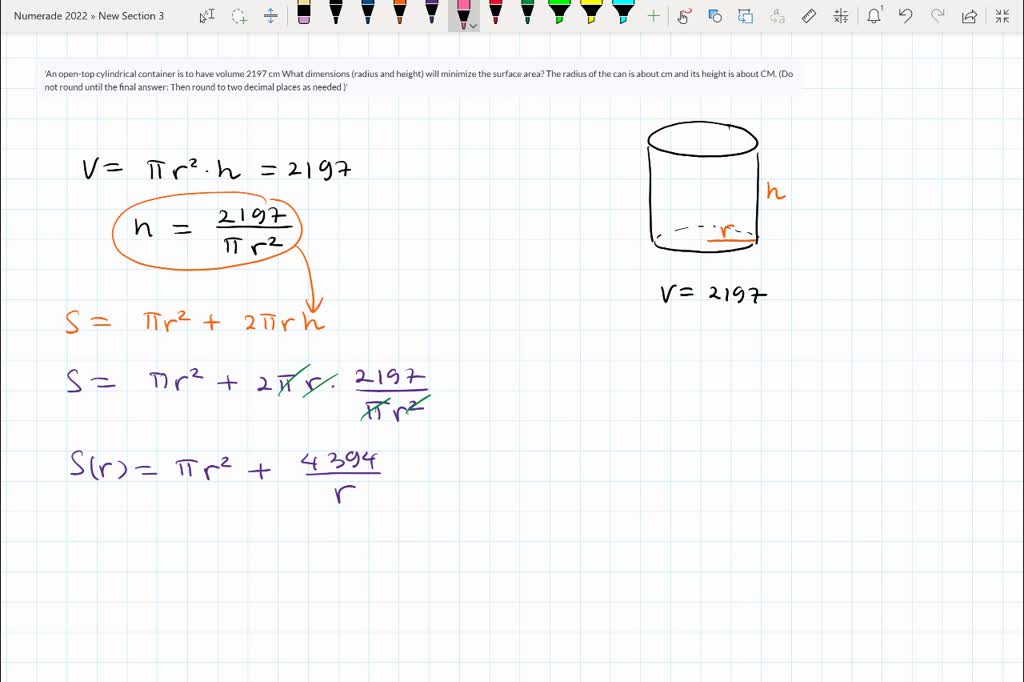
Steps to solve optimization problems. How to minimize the surface area of a box. Find the radius and height of a soda can with.

Minimizing surface area for a given volume. To minimize surface area of integer cuboid of the known volume. This will help us in finding formulas for the total surface area and volume.

(a) express the surface area s of the box as a function of x. Consider the following algorithmic task: Maximizing the area of a garden.

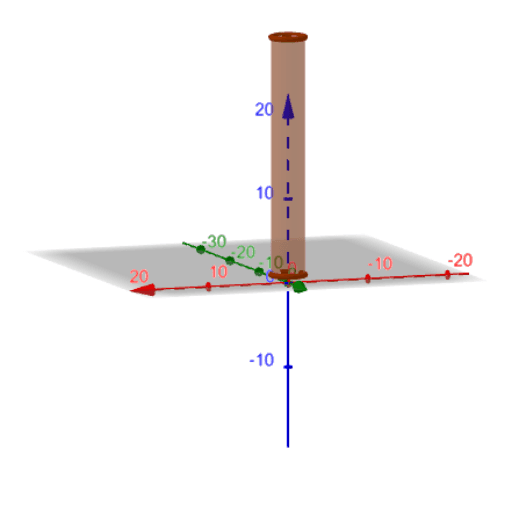
What is the minimum surface area? A typical goal for designing a can would be to minimize the surface area (in order to minimize the amount of material needed). The silo will have some radius r, and its cylindrical.

Our first task is to draw a sketch of the silo; If you have ever wondered how to find a surface area. Asked 9 years, 5 months ago.

There is a cuboid (a * b. Step 4 (use calculus to optimize): Use the slider to adjust the shape of the cylinder and watch the surface area fluctuate about the minimum of the surface area function.

To find the can's minimum surface area, we turn to calculus and start by differentiating \(s(r)\) with respect to \(r\): 23k views 6 years ago calculus i (limits, derivative, integrals) **full course** description: